by Harold Hobson.

To your everyman in the street, mathematics is all about numbers. Numbers, to many people, are difficult to work with and some even find them boring. For them, math is something they survived in school and few memories of their math are happy ones. So who invented this difficult subject? And why?

I don’t see it that way. Yes, numbers are a part of what math is about. But math is more often about patterns. And sometimes, but not always, numbers are what gives patterns their shape or substance. 

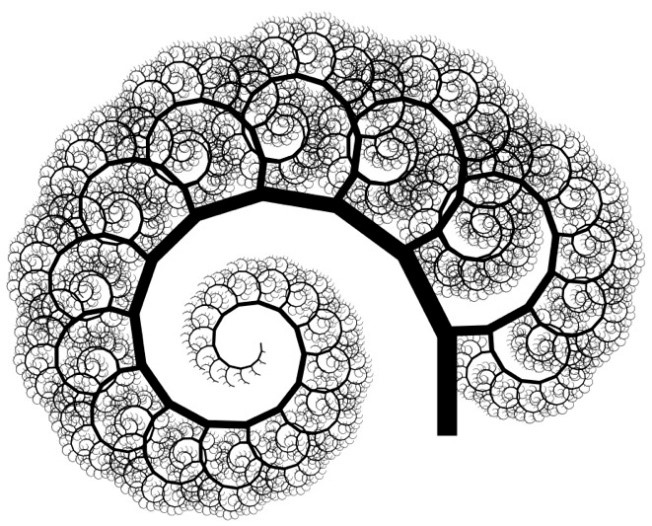
 Let’s look at an interesting set of geometric patterns in mathematics, known as fractals. Fractals are very hard to define precisely, but most are linked by a set of four common fractal features: intricacy, zoom symmetry, complexity from simplicity and fractional dimensions. Here are two examples of fractal patterns in mathematics.

 In each case, one can clearly see how a simple shape can be repeated recursively, and infinitely, to form a pattern that becomes increasingly smaller and also increasingly complex. This is the nature of fractal patterns in mathematics. 

But, speaking of nature, did you know that fractal patterns also exist in nature? The next time you look at a fern, take note of its fractal features. Note how a simple shape is repeated in ever smaller copies of itself. The entire fern is built up from the same basic shape repeated over and over again at ever smaller scales, from the branches, to the fronds and the leaves, right down to the veins in each leaf.

Fractals are found elsewhere in nature too. All of the following pictures show fractals.

 Trees, feathers, drying clay mud, snowflakes, lightning and river deltas are all examples of fractals in nature.

• 

• 

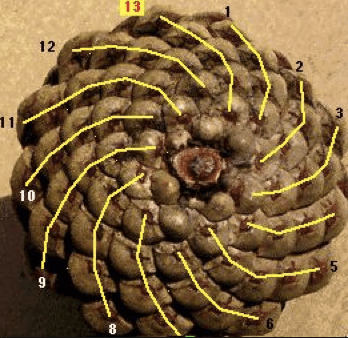
Sometimes fractal patterns in nature are combined with numbers to show convincingly that mathematics is at work in nature. In 1202 AD, an Italian number theorist called Fibonacci discovered a number sequence, while trying to mathematically plot the growth rate of rabbit populations. In this sequence, each number is made from the sum of the previous two numbers. So the sequence looks like this. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89….. and so on. Although not the first person to discover this sequence, he is the one with whom it is associated, hence it is called the Fibonacci sequence. The amazing thing is that numbers from the Fibonacci sequence (also known as the Fibonacci series) keep on cropping up in nature, especially in spirals, such as pinecones, sunflowers and seashells. And spirals are yet another example of fractals!

• 

• 

 The next time you pick a flower, take note of how many petals it has. Chances are it will be a Fibonacci number!

The other amazing fact is that if you divide any number on the Fibonacci series by the number before it on the series (it doesn’t work with the smallest Fibonacci numbers), the result is approximately equal to 1.618, known as the Golden Constant or Golden Ratio. For example, 89 ÷ 55 = 1.6181818. The Golden Ratio is considered a most pleasing artistic proportion and is found in many examples of art and architecture.  It is also found repeatedly, in nature, including in the human body.

I have barely scratched the surface of showing you the mathematics of our everyday world, but space doesn’t allow me more. Although we don’t know where mathematics comes from and we also don’t know why mathematics shows up so often in nature, we can recognize that nature takes on certain patterns that point to nature not being random, but rather led by design. It shows us that mathematics is not a construction of mankind but has been around for far longer than Man has been able to count and recognize patterns. Far from being difficult and boring, Mathematics is full of wonder and interest. Mathematics is everywhere, it’s all around us, you just have to look at the world around us with new eyes to see it!  

Mr. Hobson, Grade 6 Homeroom teacher and Math and Individuals and Societies Teacher.